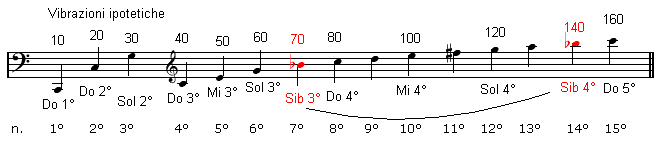
Gli accordi sono costruiti in base al principio delle terze sovrapposte, quindi non sono stati creati secondo il frutto dell’immaginazione di qualche musicista, si può dire che la musica è matematica. Ogni corpo sonoro, quando vibra produce il suono principale emettendo anche dei suoni secondari più deboli che si mescolano con il suono principale. Da qui nascono i suoni armonici che non vengono rilevati nal nostro orecchio umano, però è possibile risalire ad essi tramite gli oscillografi a raggi catodici. Nell’immagine in baso trovate i suoni prodotti dalla nota Do1°:
Ad ogni armonico assegneremo un numero ipotetico di Hertz in modo da semplificare le operazioni matematiche, considerando che la nota La3°, che si trova fra il 6° e il 7° armonico produce esattamente 440 Hertz, (si tratta del diapason).
__________________________________
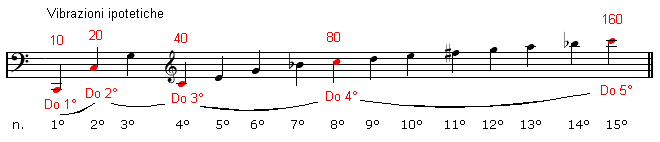
Nell’immagine sottostante potete notare la nota Do1° alla quale sono state assegnate 10 hertz (vibrazioni ipotetiche). Moltiplicando questo numero x2 si ottiene l’ottava Do2° = 20 vibrazioni.
Moltiplicando il numero ottenuto x2, si ottiene anche in questo caso l’ottava esatta Do3° = 40 vibrazioni, e così via. Quindi da questo potete capire che moltiplicando le vibrazioni di un qualsiasi suono alla 2ª, si ottiene la sua ripetizione di un ottava più alta.
Riflettendo:
Il 3° armonico presenta delle vibrazioni 3 volte maggiori rispetto al 1° armonico.
Sol 2° raddoppia le vibrazioni ad ogni ottava
Il 4° armonico che è il raddoppio del 2° che lo era del 1°
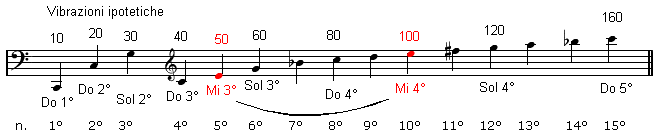
Il 5° offre il quintuplo (50) delle vibrazione assegnate al 1° armonico, vedi in basso
Con il 5° armonico si ottiene l’accordo maggiore completo, anche con il Mi 3° le vibrazioni raddoppiano ad ogni ottava.
Il 6° armonico è il raddoppio del 3°, mentre il 7° che fin ora non era presente, offre un numero di vibrazioni maggiori di sette volte, quindi è un intervallo di settima minore.
(Nota: gli armonici 4, 5 e 6 offrono un accordo maggiore perfetto che inieme al 7° armonico danno vita ad un accordo di 7ª minore).
Grazie alla 2ª operazione è possibile perfezionare il calcolo degli hertz di tutti gli armonici:
1° armonico – Do1° = 10 vibrazioni
2° armonico – Do2° = 20 vibrazioni
3° armonico – Sol2° = 30 vibrazioni
4° armonico – Do3° = 40 vibrazioni
5° armonico – Mi3° = 50 vibrazioni
6° armonico – Sol3° = 60 vibrazioni
7° armonico – Sib3° = 70 vibrazioni
8° armonico – Do4° = 80 vibrazioni
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bassi, FX e Amp
|
Amp. e FX per chit.
|
Mixer |
|
|
|
|
|
|
| Batterie e Perc
|
Strumenti per DJ |
||
|
|
|
|
|
|
Microfoni |
Lighting
|
Tastiere e Pianoforti |
Negozio di strumenti musicali online - vendita al miglior prezzo e numerose offerte
